The odds of a correct first guess in Clue
09 September 2020 ·Prompted by a strange dream, I decided to calculate what your odds are of correctly guessing the three pieces of evidence the first time in the game of Clue.
In practice, successfully doing this is likely to provoke accusations of cheating. But a simple calculation will show that this is likely undeserved. In a standard game of Clue1, there are six character cards, six weapon cards, and nine location cards. Without any information at all, that gives the odds of correctly guessing on your first turn at only 1/6 × 1/6 × 1/9 = 1/342, which is frequent enough that anyone who plays Clue many times is likely to encounter it. Keep in mind that each player has these odds on their first guess, which significantly raises the chances of ever seeing it happen in a game.
Of course, in every game of Clue each player will have some evidence, and so the odds of a correct first guess go up quite a bit. How much? That depends on how much evidence (how many cards) you receive.
The rules for the distribution of evidence are pretty simple. The three “correct” cards are removed from the deck of evidence, it’s shuffled, and distributed to players as evenly as possible. The players then proceed to interrogate each other about the cards they have, in order to eliminate live possibilities about the correct combination of person, weapon, and location. You hope to eliminate all but one combination (the correct one) before any other player can do so. In my circles, when children are playing, the players are arranged so that the younger will receive more cards than the older if they can’t be divided evenly.
Not every combination of cards is equally likely. If you are to receive five cards, you’re most likely to receive two of two of the card types and one of the third, or three locations, one weapon, and one person. These five-card hands are dealt a combined 58% of the time! In addition, some hands make a correct first guess easier than others: for a five-card hand, the best hand (all characters or all weapons) gives you almost three times better odds than the worst one (four locations, one other card). Note that actually, the better hands tend to be heavy in locations because you have to visit fewer of them. A low-location hand only improves your chances of guessing blindly.
Okay, so what we have to do is figure out the odds of each hand combination (multiset), and multiply that by the chances of a correct first guess for each hand, and sum up the results to get the total odds of a correct first guess (assuming a perfectly shuffled deck). I wrote Python code to do that here.
Now, here are the results! Some of the hands aren’t possible, because standard clue only supports six players, which means each of them would get three cards, but I’ve included “odds” games, where a player might start out with zero to two instead.
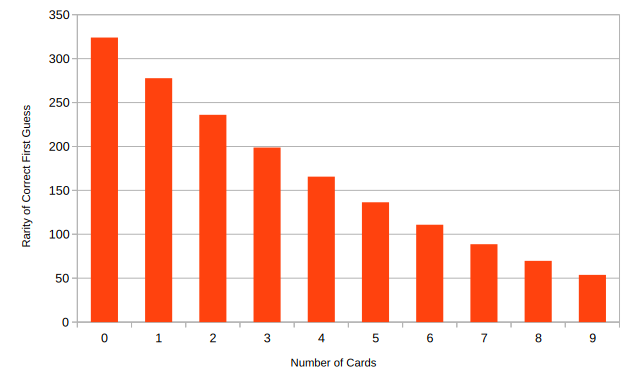
So for a five card hand, you’d expect to guess correctly the first time about once every 136 games. With six cards that drops to once every 111 games! Combining these facts with multiple players, you can show that fair games of clue will end with a player solving the mystery on their first turn every 30-40 games.
A Clue bot?
Thinking about this problem made me consider writing a Clue bot, but I ended up deciding against it. It might be an interesting project: you can do a very good approximation of perfect play with a bot that just tabulates its knowledge about every player’s hand and uses a simple pathfinding algorithm to efficiently traverse the board.
However, there are two good reasons not to bother. One is that Clue isn’t a “fair” game: an improved strategy may reduce your win rate rather than improve it. (In this specific sense, both Chess and Candy Land are fair.) The reason for this is that the standard rules of Clue say:
To make a Suggestion, move a Suspect and a Weapon into the Room that you just entered.
Normally, moving around the board is a slow process, since rooms are fairly far apart and you only get to move one d6 each turn. (This also adds quite a bit of luck into the game.) However, because the murder suspects are also other players, the above rule means that each guess (“Suggestion”) you make will instantly teleport one of them into the room with you. This can either aid (by vastly reducing travel time) or harm (by preventing an intended move) another player.
With coordination among the other players, it’s possible to harass one player and make it almost impossible to plan movements. Even without this unfair practice, it’s often in the interest of individual players to harass those of equal or greater skill to them. That’s just clever play! This can backfire, of course, but the better a player (or bot) is, the more likely other players are to attempt it, and it can make intelligent pathfinding impossible.
There’s a simpler reason not to bother with a bot, however, and that’s that close to perfect play is already easily achievable by humans. We’re already pretty good at intuiting optimal routes, and extracting as much information as possible from gameplay is easily done with an algorithm:
The game comes with worksheets for the players to use which list every card in rows, and have several columns (probably intended to save paper over multiple games). Simply assign the first column to yourself, and every succeeding column to the other players in the order of play. The additional columns are used to collect any information you can obtain about what hands the other players have. At the top of each column write the number of cards that player has. Use your own column to summarize everything you know about the solution. An “x” means that you know that a card is not part of the solution, and a box means that you know it is.
For the other columns, a box means that the player does not have the corresponding card. An “x” means that they do (and therefore, that there should also be an “x” in your column, the “solution” column). Whenever a player is not able to show any cards to someone (including you), place the box in each of the rows for that player. When a player shows a card to someone besides you, place a tiny number in that column in any row they might have a card in. (Simply increment the number you use in each column every time you need a new one.) Whenever logic forces you to place a box in someone’s column, check to see if only one row that shares a number remains, and you can then put an “x” there. If you can work out every card that a player has, you can put a box in every other row.
Example: Player 1 suggests Ms. Scarlet, the candlestick, and the ballroom. Player 2 has none of these cards, so you put a box on each one in their column. Player 3 shows a card, so you put a “1” in each box in their column. Player 2 suggests Ms. Scarlet, the knife, and the kitchen. Player 3 has none of these cards, so you now have a box for Ms. Scarlet in their column. It comes around to your turn, and you suggest Mr. Green, the candlestick, and the library. Player 1 shows you the candlestick. So you put an “x” on their column for candlestick, which means a box belongs in Player 3’s column for the candlestick. Now you’re only left with one “1” in that column, on the ballroom. So you know Player 3 must have shown Player 1 that card and so you can put an “x” in the box. Now you know it’s not part of the correct solution!
Obviously there’s a bit more improvement you can do with ideal guessing, and it might make sense to keep track of what other players know so you can surmise if they’re about to make a correct accusation, in which case you might want to jump the gun if you have a 50/50 shot. But 95% of strategy can be easily implemented by a player following the approach above.
